“死神永生。”

顺着门一路行走，程心与关一帆进入了647号小宇宙，智子迎接了他们。 太阳系被二维化仿佛还在昨日，但已经是亿万年前的往事；DX3906下的蓝星被死线割裂的记忆，也随着沧海桑田般的变换葬在尘埃里。

程心以公元人的身份，经历了一生颠沛流离悲欢离合，目睹了人类文明的跌宕起伏消弭殆尽，主导了救赎，赋予了希冀，又亲手把一切努力葬送。身世浮沉恩恩怨怨是是非非，恍如昨日大梦一场，醒来内心也毫无悸动，只觉木然。

不过，在这与世隔绝的仙境，程心逐渐缓和了她恐惧不安的情绪，和关一帆和智子在一起，多少也有一个陪伴。除了耕作，学习新的知识，书写《时间之外的往事》，程心还培养起了一个爱好：下国际象棋。 这来自上古西方的游戏，用64个格子、32个棋子，在黑白交加的棋盘上演绎着王国腾飞到衰落，又或者是破碎到复兴，她觉得，这像极了过去。 程心当然不会去和智子下棋，毕竟和机器下棋毫无胜算；然而关一帆的棋艺远在程心之上，纵使她绞尽脑汁竭尽全力也赢不了他一局。于是程心决定研究一些别的与国际象棋有关的问题。

（以下进入正文）

程心在小宇宙的微型电脑中查阅公元时期资料时，定位关键词21世纪、国际象棋、算法竞赛，她搜到了如下题目：

[SCOI2005] 互不侵犯 ：研究国王互相攻击的问题

[2019年雅礼集训] ROOK：研究车互相攻击的问题

[USACO1.5] Checker Challenge：研究皇后相互攻击的问题

[SCOI2005] 骑士精神 ：研究骑士的行走问题

她发现，没有任何研究象（主教）和兵的问题。她觉得兵的问题没有什么可以研究的，所以她决定研究象的互相攻击问题。

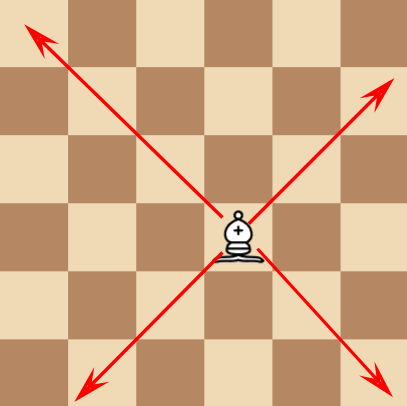
国际象棋中的象的吃子规则是，只能沿着所在的斜线吃子。以6x6棋盘中的一个象为例，这个象可以攻击到箭头表示的这四个斜线方向任何一个格子。

具体地，程心提出了这样一个问题： 对于一个大小为 $N×N$ 的棋盘，在这个棋盘上放置 $K$ 个国际象棋中的象，并且这 $K$ 个象不能互相攻击到，求有多少种放置的方案数。两种方案数不同，当且仅当这两种方案中，存在一个格子满足第一种方案在这个格子上有象，而第二种方案在这个格子上没有象。

程心觉得这是一个好的问题，她把关一帆和智子叫过来一起研究。但是智子非常不屑，因为以她的运算能力，可以把所有情况直接穷举出来。但是为了让两个人类朋友接受她的运算结果，她需要自己设计一个高效的算法。由于数字可能太长，只需要提供答案对 $998244353$ 取模的结果即可。

智子想知道，这个算法应该如何设计呢？

第一行两个数字 $N,K$，表示棋盘规模和象的个数。$2\le N\le 10^3,1\le K\le 2N-2$。

输出共一行，第一行输出一个整数，表示方案数对 $998244353$ 取模的结果。

两个象可以分别放在$(1,1), (1,2)$ 或$(1,1), (2,1)$ 或$(1,2), (2,2)$ 或$(2,1), (2,2)$共 $4$ 种方案。