2023年12月15日，也就是两天前，发生了一个重大事件 —— 《戴森球计划：黑雾崛起》正式上线！

作为一名热衷于建造戴森球的玩家，咸鱼鱼立刻投身进了这场新的史诗。

但是，他在面对“黑雾”这一种新的敌人时，遇到了一些难题······

我们将游戏地图看作一个平面直角坐标系，每个单位或者建筑都只会在坐标系中的整点上。

玩家的基地位于坐标原点 $(0, 0)$，生命值为 $P$。

地图中有 $A$ 个炮塔，每个炮塔的坐标为 $(X_i, Y_i)$，攻击力为 $Z_i$。

地图中有 $B$ 个敌人，每个敌人的坐标为 $(U_i, V_i)$，攻击力为 $W_i$，生命值为 $H_i$

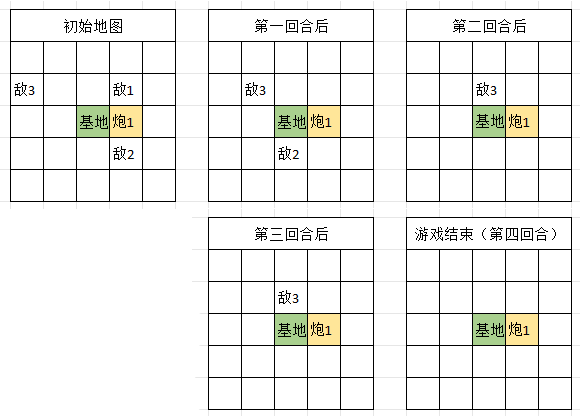
接下来，我们将游戏过程抽象为 $N$ 回合，每回合按照如下顺序行动：

1. 炮塔按编号从小到大依次行动。第 $i$ 个炮塔会选取离它 曼哈顿距离最近 的敌人作为目标，如果有多个距离最近的目标，则选择 编号最小 的目标。第 $i$ 个炮塔会使得该敌人的生命值减少 $Z_i$。如果一个敌人的生命值 小等于 $0$，那么该敌人死亡（该敌人从游戏中移除，不参与任何后续的过程）。
2. 敌人也按编号从小到大依次行动。如果第 $i$ 个敌人距离基地的 曼哈顿距离 小于等于 $1$，那么该敌人会攻击基地，使得基地的生命值减少 $W_i$；如果第 $i$ 个敌人距离基地的 曼哈顿距离 大于 $1$，那么该敌人会往基地移动，移动时敌人会先向 $y$ 轴移动，再往坐标原点移动（即优先减少距离基地的横坐标差值，其次才减少纵坐标差值）。如果基地的生命值小于等于 $0$，则基地被摧毁，游戏结束。

游戏结束的条件共有三种：敌人全部死亡、基地被摧毁、游戏已经进行了 $N$ 轮。

如果游戏因为敌人全部死亡而结束，则输出 两行，第一行为"Win"，第二行为两个正整数，分别表示游戏结束时的 回合数 和 基地剩余的生命值。

如果游戏因为基地被摧毁而结束，则输出 两行，第一行为"Lose"，第二行为两个正整数，分别表示游戏结束时的回合数 和 剩余的敌人数量。

如果游戏因为已经进行了 $N$ 回合而结束，则输出 两行，第一行为"Draw"。第二行为两个正整数，分别表示 基地剩余的生命值 和 剩余的敌人数量。

因为在构思本题时，黑雾崛起尚未发售，所以我们假设所有的炮塔、敌人和基地，都是允许重合的（即允许位于同一坐标）。

曼哈顿距离 的定义为：若两个点的坐标分别为 $(x, y)$ 与 $(u, v)$，则这两个点的曼哈顿距离为 $|x-u|+|y-v|$，其中 $|x|$ 表示 $x$ 的绝对值。

输入共有 $1+A+B$ 行。

第一行包含四个正整数 $N, A, B, P\ (1 \leq N, A, B \leq 100, \ 1 \leq P \leq 10000)$，分别表示游戏的最大回合数、炮塔数量、敌人数量和玩家基地生命值。

接下来的 $A$ 行，其中的第 $i$ 行包含三个正整数 $X_i, Y_i, Z_i \ (0 \leq |X_i|, |Y_i| \leq 100, 1 \leq Z_i \leq 100)$，分别表示第 $i$ 个炮塔的坐标和攻击力。

接下来的 $B$ 行，其中的第 $i$ 行包含四个正整数 $U_i, V_i, W_i, H_i \ (0\leq |U_i|, |V_i| \leq 100, 1 \leq W_i, H_i \leq 100)$，分别表示第 $i$ 个敌人的坐标、攻击力和生命值。

如果游戏因为敌人全部死亡而结束，则输出 两行，第一行为"Win"，第二行为两个正整数，分别表示游戏结束时的 回合数 和 基地剩余的生命值。

如果游戏因为基地被摧毁而结束，则输出 两行，第一行为"Lose"，第二行为两个正整数，分别表示游戏结束时的回合数 和 剩余的敌人数量。

如果游戏因为已经进行了 $N$ 回合而结束，则输出 两行，第一行为"Draw"。第二行为两个正整数，分别表示 基地剩余的生命值 和 剩余的敌人数量。

对于样例 $1$ 来说，游戏最多进行 $5$ 回合，每回合的地图如下。基地在第三回合受到了一点伤害。