传说将数字注入虚空，古代的冰雪魔法使可以编织出数字魔法雪花：每片孤立的花瓣，仅携带着一个原始数字的力量。随着魔法造诣的提升，他们逐渐掌握了更复杂的法术，能够晋升数字魔法雪花的阶数，使雪花的复杂度都会呈几何级数增长，且每片花瓣都需要更多的数字来维持其存在。

具体的，对于一阶完整数字雪花，定义是由 $6$ 个数字按正六边形、从正上方顶点开始、逆时针的排列；而对于 $n$ 阶完整数字雪花，递归地定义它是由 $6$ 个 $n-1$ 阶完整数字雪花按正六边形、从正上方顶点开始、逆时针的排列，而构成它的 $6$ 个 $n-1$ 阶完整数字雪花我们称作是它的花瓣。下图是一个二阶完整数字雪花（$6$ 个花瓣）。

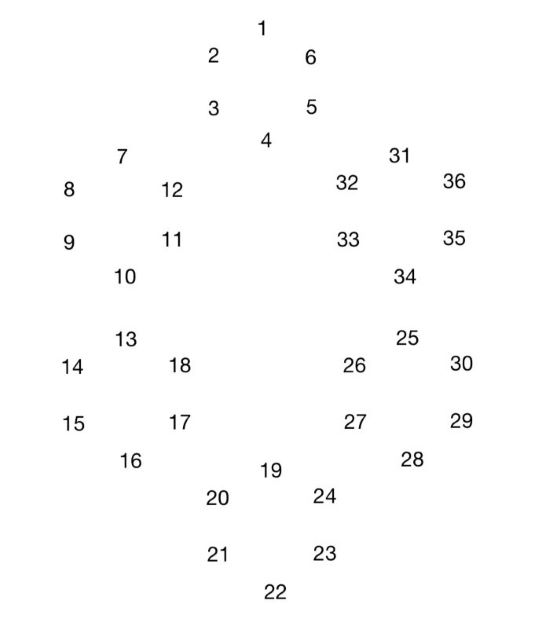
当然，世界上没有事物总是完美的。即使某个完整数字雪花缺少了一部分数字，只要它包含两个或以上不同的 $n-1$ 阶完整数字雪花的任意部分，我们称作它是 $n$ 阶不完整数字雪花，而这些 $n-1$ 阶雪花的部分我们称作是它的花瓣。特别地，对于一阶完整或不完整数字雪花，组成它的数字即为它的花瓣。下图是一个二阶不完整数字雪花（$3$ 个花瓣，因为它包含了三个一阶完整数字雪花的某些部分）。

烤鱼鱼作为新一代的冰雪魔法使，他接下了由远古冰雪魔法使继承的任务，继续深造编织数字雪花的魔法。经过了不懈的努力，终于有一天，烤鱼鱼有幸让冰雪魔法界最强大的雪花——魔法数字雪花重现于世，因为魔法数字雪花是一个由非零自然数排列的无穷阶的数字雪花！然而烤鱼鱼的魔法力终究有限，他只能展现魔法数字雪花的数字区间为 $[a,b]$ 的部分——一个 $k$ 阶完整或不完整数字雪花。

由于魔法数字雪花的内部结构过于错综复杂，烤鱼鱼看不清这个雪花的所有细节，因此他只关心他生成的数字雪花有几个花瓣。魔法使烤鱼鱼已经知道了自己的魔法力可以重现数字区间为 $[a,b]$ 部分的魔法数字雪花，你能帮他计算这个 $k$ 阶数字雪花有多少个花瓣吗？

第一行输入一个整数 $T$ 表示题目的测试数据的组数。

紧接着输入 $T$（$1 \leq T \leq 10^{5}$）行，每行输入两个正整数 $a, b$（$1 \leq a < b \leq 10^{12}$），表示烤鱼鱼展现魔法数字雪花的数字区间为 $[a,b]$。

输出 $T$ 行，每行输出一个 $1$ 到 $6$ 整数，表示烤鱼鱼能看清的魔法生成雪花的花瓣数量。

对于第一组数据，$1$ 到 $36$ 构成一个 $2$ 阶完整数字雪花，那么它有 $6$ 个花瓣。

对于第二组数据，$28$ 到 $30$ 构成一个 $1$ 阶不完整数字雪花，数字个数即为它的花瓣个数。

对于第三组数据，$13$ 到 $24$ 构成一个 $2$ 阶不完整数字雪花，其中 $13$ 到 $18$ 组成第一个花瓣, $19$ 到 $24$ 组成第二个花瓣。

对于第四组数据，$18$ 到 $73$ 构成一个 $3$ 阶不完整数字雪花， 其中 $18$ 到 $36$ 组成第一个花瓣, $37$ 到 $72$ 组成第二个花瓣，$73$ 组成第三个花瓣。