Pashmak's homework is a problem about graphs. Although he always tries to do his homework completely, he can't solve this problem. As you know, he's really weak at graph theory; so try to help him in solving the problem.

You are given a weighted directed graph with n vertices and m edges. You need to find a path (perhaps, non-simple) with maximum number of edges, such that the weights of the edges increase along the path. In other words, each edge of the path must have strictly greater weight than the previous edge in the path.

Help Pashmak, print the number of edges in the required path.

The first line contains two integers n, m(2 ≤ n ≤ 3·10⁵; 1 ≤ m ≤ min(n·(n - 1), 3·10⁵)). Then, m lines follows. The i-th line contains three space separated integers: u_i, v_i, w_i(1 ≤ u_i, v_i ≤ n; 1 ≤ w_i ≤ 10⁵) which indicates that there's a directed edge with weight w_i from vertex u_i to vertex v_i.

It's guaranteed that the graph doesn't contain self-loops and multiple edges.

Print a single integer — the answer to the problem.

In the first sample the maximum trail can be any of this trails: .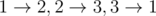

In the second sample the maximum trail is .

In the third sample the maximum trail is 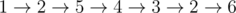.