Line Graph $L(G)$ can be considered as an operator on an undirected graph $G$ just like Complementary Graph and Dual Graph.

Rikka generalizes Line Graph to edge-weighted undirected graphs. For a graph $G=\langle V,E\rangle$, $L(G)$ is still an edge-weighted undirected graph which is constructed in the following way:
1. $L(G)$ has $|E|$ vertices and the $i$th vertex corresponds to the $i$th edge in $G$.
2. There is an edge between $i,j$ in $L(G)$ if and only if edge $i$ and $j$ have at least one common vertices in $G$. And the edge weight is equal to the sum of the weights of edge $i$ and $j$ in $G$.

For example, in the following picture, the right graph is the line graph of the left one. Vertex $1,2,3,4$ in $L(G)$ correspond to edge $(1,2),(1,4),(1,3),(3,4)$ in $G$. And if all edges in the left graph have weight $1$, the edges in the right graph will have weight $2$.


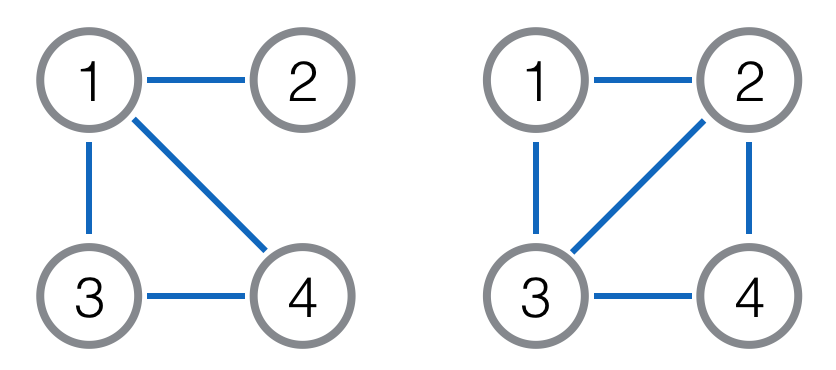
Now, Rikka has an edge-weighted tree $T$ with $n$ vertices. And she constructs a graph $G=L(L(T))$. It is clear that $G$ is connected.

Let $d(i,j)$ be the length of the shortest path between vertex $i,j$ in $G$(the length of each edge is equal to the weight), $m$ be the number of vertices in $G$, Rikka wants you to calculate $\sum_{i=1}^m \sum_{j=i+1}^m d(i,j)$.

The first line contains a single number $t(1 \leq t \leq 100)$, the number of the testcases.

For each testcase, the first line contains one single integer $n(1 \leq n \leq 10^5)$.

Then $n-1$ lines follow, each line contains three integers $u_i,v_i,w_i(1 \leq u_i,v_i \leq 10^5, 1 \leq w_i \leq 10^9)$, describe an edge with weight $w_i$ between $u_i$ and $v_i$.

The input guarantees that $G$ has at least one vertices and there are at most $5$ testcases with $n>10^3$.

For each testcase, output a single line with a single number, the answer modulo $998244353$.