Problem C. geometric problem
时间限制 1000 ms 内存限制 256 MB
There are six points $ABMNXY$ in a two-dimensional plane.
As shown in the figure below, $ABNM$ and $XYNM$ are both in convex quadrilateral shapes, and their intersection area is $0$. You are also given two lines $L1$ and $L2$. You have to choose one point on each line (for example, $S$ on $L1$ and $T$ on $L2$) so that the area of $ABS$, $MSNT$, and $XYT$ are at the same size. Moreover, $S$ should lie within or be on the border of $ABNM$, and $T$ should lie within or be on the border of $XYNM$. Please output the positions of $S$ and $T$ that you choose!
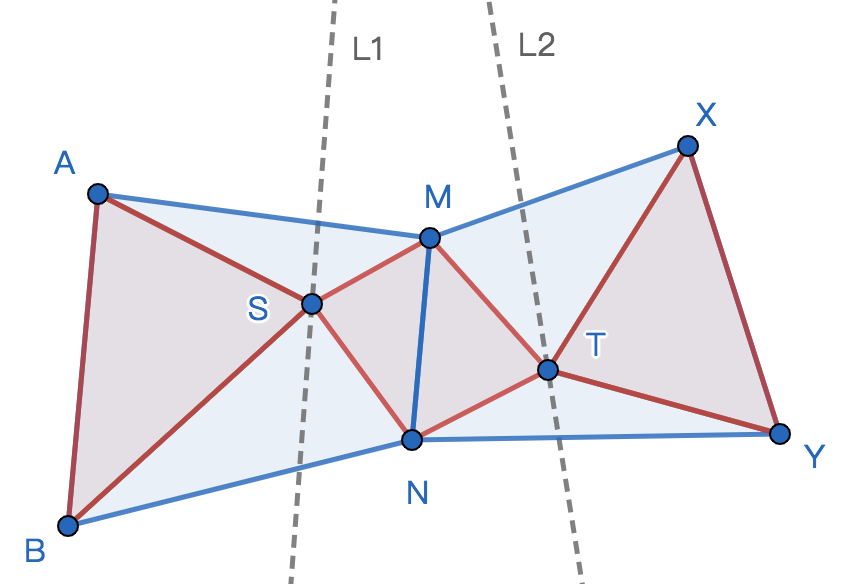
As shown in the figure below, $ABNM$ and $XYNM$ are both in convex quadrilateral shapes, and their intersection area is $0$. You are also given two lines $L1$ and $L2$. You have to choose one point on each line (for example, $S$ on $L1$ and $T$ on $L2$) so that the area of $ABS$, $MSNT$, and $XYT$ are at the same size. Moreover, $S$ should lie within or be on the border of $ABNM$, and $T$ should lie within or be on the border of $XYNM$. Please output the positions of $S$ and $T$ that you choose!

输入数据
The first line contains an integer $T$ indicating the number of test cases.
Each test case consists of three lines. The first line contains $12$ integers, $A_x, A_y, B_x, B_y, M_x, M_y, N_x, N_y, X_x, X_y, Y_x, Y_y$, denoting the $x$ and $y$ coordinates of points $A,B,M,N,X,Y$. The second line contains $4$ integers, $L1_{1,x}, L1_{1,y}, L1_{2,x}$, and $L1_{2,y}$, denoting two distinct points on $L1$. The third line also contains $4$ integers, $L2_{1,x}, L2_{1,y}, L2_{2,x}$, and $L2_{2,y}$, denoting two distinct points on $L2$.
* $1 \le T \le 20$
* coordinates are in the range $[0, 514]$
* $L1_1 \neq L1_2$, $L2_1 \neq L2_2$
Each test case consists of three lines. The first line contains $12$ integers, $A_x, A_y, B_x, B_y, M_x, M_y, N_x, N_y, X_x, X_y, Y_x, Y_y$, denoting the $x$ and $y$ coordinates of points $A,B,M,N,X,Y$. The second line contains $4$ integers, $L1_{1,x}, L1_{1,y}, L1_{2,x}$, and $L1_{2,y}$, denoting two distinct points on $L1$. The third line also contains $4$ integers, $L2_{1,x}, L2_{1,y}, L2_{2,x}$, and $L2_{2,y}$, denoting two distinct points on $L2$.
* $1 \le T \le 20$
* coordinates are in the range $[0, 514]$
* $L1_1 \neq L1_2$, $L2_1 \neq L2_2$
输出数据
For each test case output $4$ numbers in a single line, $S_x, S_y, T_x, T_y$, denoting the two chosen points. If there are multiple solutions, output the one with the smallest $S_x$. If there are still multiple solutions, output the one with the smallest $S_y$, and then the smallest $T_x$, and then the smallest $T_y$. Otherwise, if there are no solution, output "-1" (without quotes) in one line. A solution with an absolute error at most $10^{-6}$ will be accepted.
样例输入
复制
1
0 10 0 0 5 10 5 0 10 10 10 0
0 0 5 10
5 0 10 10样例输出
复制
3.333333333333 6.666666666667 6.666666666667 3.333333333333$ Mathjax font initiator $
提交
请先 登录